引言
现在考虑一个场景——你正在计算拿五本书和三个苹果需要多少钱。书25元一本,苹果6元一个。那么这个式子就可以列为:25*5+3*6=125+18=143。在这个过程中,你需要先记住25*5=125,再记住3*6=18。我们一般怎么称呼这个短暂的记忆过程呢?是工作记忆(working memory)。
工作记忆是大脑的一项基本认知功能。进一步地,当需要临时记住一连串的有顺序的内容时,就会涉及到同时对事件(item)及顺序(rank)的记忆。那么大脑是如何处理一系列复杂信息的呢?中国科学院脑科学与智能技术卓越创新中心的王立平教授、上海脑科学与类脑研究中心的闵斌教授、北京大学的唐世明教授的团队通力合作,用双光子钙成像记录了猕猴大脑前额叶皮层的神经群体活动,他们发现神经元群体的活动可以被降维成一些正交的环状几何结构子空间。记录得到的序列记忆并非遵循传统认知里的时序表征假说,而是具有并行性和持续性;该项研究还进一步拓展了序列工作记忆的增益调制理论。其结果在2022年发表在Science上,题为Geometry of sequence working memory in macaque prefrontal cortex.
序列编码和工作记忆
让我们先从常见的序列编码模式开始考虑。在19世纪初,神经生物学家们就在思考序列信息的编码方式。大脑有很多活动是和时序信息有关的。例如描述一本书里的内容时,要有顺序有逻辑地表述清楚书本中的内容,给别人指路时,要按顺序指明路线等等……在相似的情况下,不仅单个内容需要记住,他们之间的顺序也不能被混淆。在应用方面,能提取人类语言、精准给出检索结果的搜索引擎通常有序列信息提取的算法;最近基于序列估计原理所开发出的AI工具ChatGPT也由于其出色的语言生成能力而大受欢迎。
对于人类来说,在进行新的序列信息的处理时,大脑会暂时存储序列信息。这种短期的信息存储方式被称为工作记忆(working memory)。工作记忆是短期记忆的一种形式,例如记住一个事项清单、一串电话号码;也同时适用于我们第一次学习一系列复杂的动作:例如游泳和花样滑冰。在这种情况下,我们大脑的前额叶皮层用一组神经元将复杂信息分割成简单的较小部分,比如我们记一串电话号码时,往往会将电话号码拆分为3-4-4的组合进行记忆。上述是大脑处理序列信息的例子,但对于在时序信息记忆过程中的大脑神经编码的机制,我们知道的并不算多。
行为范式和神经元信息分解方法
猕猴社群和人类社会构建比较相似,他们的认知能力、大脑结构、功能相比于鼠、兔一类常见的实验动物更接近人类,是研究高级认知功能的最佳模型。在关于时序记忆编码的探究中,研究人员训练猕猴记忆由多个位置点依次发光组成的空间位置序列,经过提示、观看光点序列后,进入2.5-4秒的记忆延迟等待时间,猕猴需要在这段时间内记住这个序列,然后需要通过扫视的方式来“复述”这个序列。为确定猕猴的大脑神经元群在进行任务时的活动状态,研究人员对参与工作记忆的重要区域:外侧前额叶皮层进行双光子钙信号成像。钙信号用于反映神经元的脉冲放电情况,而序列信息表征的关键可能在于记忆延迟等待时间的神经元群体活动模式中。

|
图1 猕猴的序列记忆任务 |
研究人员对上述的序列记忆模式初步想法是,猕猴脑中可能也存在一个“屏幕”,猕猴将出现的点都记在这个屏幕上。但是如果存在多个带有顺序的点呢?顺序的信息是如何体现在屏幕上的?于是,考虑猕猴的大脑中是否存在不同的、和序列数目相同的多个“小屏幕”来表示序列信息。这样大脑只需要注意下一个点的位置是什么,不需要记住每一个点出现的次序,而且“小屏幕”之间不会相互干扰。为了进一步探索数据之间是否可以分离成类似的多个“小屏幕”,研究人员对钙成像组成的高维数据进行分析,发现可以在高维的钙成像数据中分离出每个序列次序所对应的子空间,也就是多个“小屏幕”。而每个子空间内,不同地点对应的空间位置和屏幕所示的环状结构也保持一致。

|
图2 子空间上的六边形 |
这暗示着前额叶皮层的神经元群体中,可能存在特定的流形——通俗来讲可以认为存在特定的“小屏幕”,在本文中可以理解为线性子空间。需要注意的是,这里的六边形并非“映照”出猕猴实际所看见的六边形,而是高维的前额叶神经元群体活动嵌入到了类似于视觉所看见的六边形图案的低维流形。随着序列信息的增加,环的尺寸进一步减小,而不同长度的序列信息对应的环是相互正交的——也就可以认为是几乎互不干扰的。
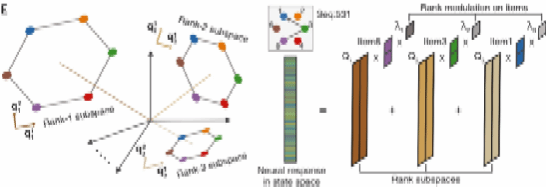
|
图3 环随着阶的变化具有的特征 |
这样的几何特征只会在2.5-4秒的记忆延迟等待时间出现,而baseline期并不会出现。而且错误的记忆结果中也不会观察到类似的环状结构。
几何特征的特征和泛化
为了进一步探究大脑是否总是用相同的“屏幕”来记忆不同类型的空间序列,研究人员对数据进行了解码分析,最终分离出相似的三个环状结构,环状结构的数量对应的是序列信息的长度。也就是说,用于编码次序的屏幕是可以通用的。
这时,细心的读者可能注意到,环的大小在不同的平面上大小不一。这并不是图像的角度问题,而是环的半径大小会随次序的增加而减小。一个可能的原因是,次序靠后的信息所得到的注意力更少,类似于我们背单词记得最熟的总是那个abandon,而其他次序靠后的单词并不能获得和前面单词同等的注意力。
不同序列空间信息是通过机器学习来训练线性分类器进行分离的。线性三层解码器的结构如下图所示。

|
图4 线性三层解码器 |
三层解码器第一层的维度是神经元个数,第二层为2,用于表示二维子空间,输出层(第三层)为6,用于表示六边形的顶点。
前面提到,不同次序的子空间中,环状结构是类似的,只是环的大小会随着次序的增加而逐渐变小。文章给出的解释是,次序靠后的信息分得的注意资源更少,从而使对应的环变小,区分度下降。这项发现可以被总结为群体水平上,空间信息编码的几何结构受到时序调制。
需要稍加注意的是,空间信息编码的几何结构受到时序调制并不适用于单个神经元水平。但是在经典工作记忆模型中,单个神经元的增益调控机制是关键假设,即:单个神经元是大脑活动的基本单元,在不同的序列活动中扮演相似的角色。这项研究启示我们,序列记忆的编码可能更需要关注群体神经元性质。
序列信息可以分解为各自的线性子空间,那么,这样的子空间是否适用于其他的序列呢?研究人员发现,如果将序列分解为序列信息-位置编码,则序列信息的子空间可以推广到其他未进行训练的序列。这里用了三个泛化分析来进一步验证。
首先,确保数据是无偏差的,使用留一交叉验证法确保未经处理的数据有一致的准确性。
其次,测试子空间是否适用于不同长度的序列。研究人员发现长度为2的序列上对长度为1和2的子空间进行训练可以推广到长度为3的序列上,反之亦然。说明这样的几何结构在不同阶的序列数据内都适用。
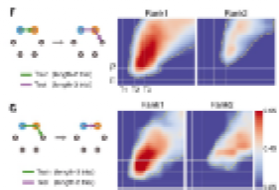
|
图5 不同的序列子空间稳定性测试 |
最后,研究人员考虑各个子空间是否互不相关。按照推断,由于秩子空间是独立的,因此每个子空间的序列检验正确与否都是独立于其他子空间的。因此,研究人员测试了在正确试验上训练的解码器是否可以推广到在相同等级上有正确反应的错误试验。发现解码效果不如前两类解码训练结果。

|
图6 正确-错误试次的解码 |
于是可以推断几何特征具有稳定性和统一性,但跨阶的训练和验证解码能力却很差,这也进一步对应了子空间的相互正交性——也就是说各个子空间是互不相关的。
研究人员对序列信号何时出现分歧很感兴趣。于是将每一刻的所有神经元信号向量投影到解码得到的子空间中,按照时间连接成连续的曲线,如下图。

|
图7 神经状态的轨迹图 |
可以看到,在初期阶段,所有神经元信号几乎都从靠近零点的位置出发,在记忆延迟期的末期,神经元信号可以在子空间中形成一个近似六边形的环状结构。于是可以想到,序列信息在起始阶段就有所分歧,随着时间的增加,序列活动所表示的结果越有特异性。
总结
三位教授的团队用拓扑几何的方法可视化了大脑对外界信息的提取方式。该研究首次在群体神经元的水平上阐释了序列工作以及编码原理,提供了一个神经网络如何进行符号表征的新思路。上世纪80年代,在人工智能领域就有使用张量积来实现神经网络对符号结构的表征这一思路,但张量积在生物学上的意义一直不甚明确。本文研究的序列工作记忆的神经表征正好可以将多而复杂的信息统一到一个低维的流形上,而且也可以将子空间对应地嵌入到高维向量空间中,与此同时,该研究的模型也支持将信息传递到下一层的神经网络上。
看似复杂的群体神经元活动可以用简洁的神经流形去描述,大数量级的群体神经元活动可以降维成小数量级上神经模态和随着时间推进而持续演变的因子。一群神经元理论上可以产生爆炸级个数的神经活动,但在生物学情况下,神经元群体处于一个低维的统一的状态——一如音乐会中的交响乐团,多个组别的乐器在指挥家的指引下发出和谐的、统一的乐音,而非杂乱的噪音。
参考文献
Xie, Y., Hu, P., Li, J., Chen, J., Song, W., Wang, X. J., Yang, T., Dehaene, S., Tang, S., Min, B., & Wang, L. (2022). Geometry of sequence working memory in macaque prefrontal cortex. Science (New York, N.Y.), 375(6581), 632–639. https://doi.org/10.1126/science.abm0204
Bernardi, S., Benna, M. K., Rigotti, M., Munuera, J., Fusi, S., & Salzman, C. D. (2020). The Geometry of Abstraction in the Hippocampus and Prefrontal Cortex. Cell, 183(4), 954–967.e21. https://doi.org/10.1016/j.cell.2020.09.031
Chaudhuri, R., Gerçek, B., Pandey, B., Peyrache, A., & Fiete, I. (2019). The intrinsic attractor manifold and population dynamics of a canonical cognitive circuit across waking and sleep. Nature neuroscience, 22(9), 1512–1520. https://doi.org/10.1038/s41593-019-0460-x
Miller, E. K., Lundqvist, M., & Bastos, A. M. (2018). Working Memory 2.0. Neuron, 100(2), 463–475. https://doi.org/10.1016/j.neuron.2018.09.023
本文作者:袁鹏组寇蓝文